「コンピュータシミュレーション」,「数値流体解析」とは?
自然界または人間社会のあらゆる変動においてその裏には,必ず何らかの因果関係(y=F(x))が存在します。このような因果関係を法則にまとめ,さらに微分ないし積分方程式という抽象的な数学モデルで表現することは,現代科学の大きな特徴であり,人類の最も誇るべき知恵の一つとも言えるでしょう。
例えば,流体を連続体として取り扱う場合には,その振る舞いを記述する数学モデル(「支配方程式」と言う)として以下のようにまとめられます。
流体運動の支配方程式
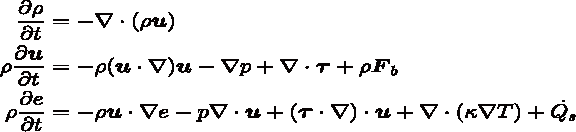
上記方程式の左辺は,それぞれ流体の状態を表す密度,速度,内部エネルギー(温度)という状態変数の時間変化率であり,それらの変化は方程式の右辺にある全ての項が代表する物理要因によって定められます。仮に,適切な初期条件・境界条件のもとでこれらの方程式を完全に解くことができれば、任意の時刻のあらゆる空間点における流体の状態が分かります。これによって,流体の振る舞いを把握し,自然現象の予測または工業製品の開発に大変役に立ちます。しかし,上記方程式右辺の各項には大変複雑な物理過程や非線形相互作用が含まれており,簡略化された理想的なモデル以外はその解を理論的に求めることができません。
一方、コンピュータの発達に伴い、様々な現象をディジタル化し、コンピュータを駆使すれば、それらの現象の振る舞いを再現すること、いわゆる「コンピュータシミュレーション」ができるようになりました。流体力学においても,「数値流体力学」(CFD: Computational Fluid Dynamics)という新しい研究分野が急速に発展し、上記の方程式の数値解を求めることで流体現象を模擬することを実現しました。
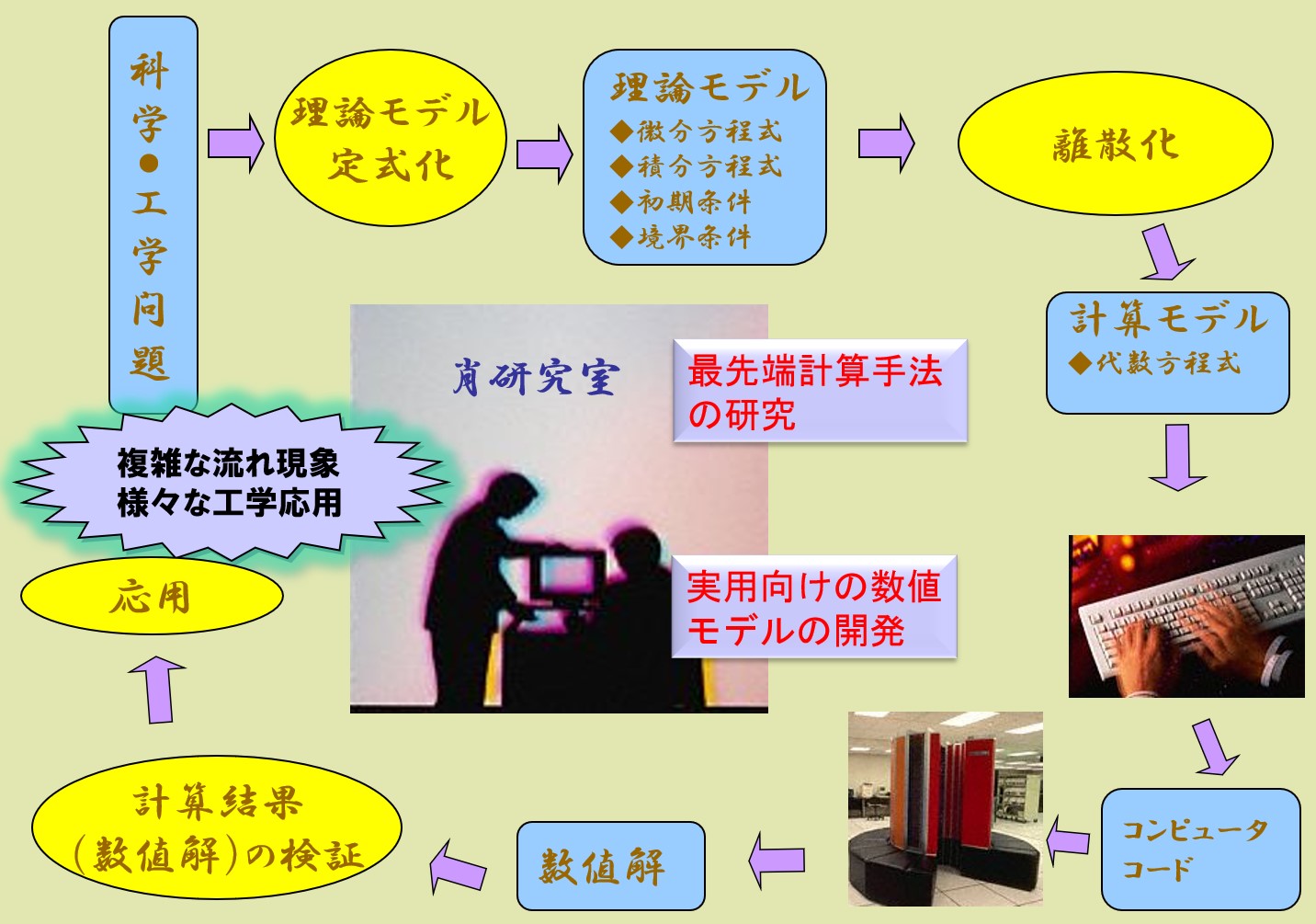
次の図に示すように,コンピュータシミュレーションあるいは数値解析の目的は、物理法則を表す数学方程式の数値解を求めることです。具体的に,以下の手順で構成されます。
研究対象となる科学や工学の問題に対し,適切な数理モデル(支配方程式+初期条件・境界条件)を検討する
計算手法(スキーム)を開発し,代数方程式y=F(x)の形で数値モデルを建てる
プログラミング言語を使ってコンピュータプログラム(計算コード)を作る
コンピュータプログラムの誤り(バグと呼ぶ)を探し,取り除く(デバッグ)
計算コードを実行し,数値解を求める
可視化などによって数値解(計算結果)を整理し,考察する
実問題に応用する
数値流体解析作業の流れ
コンピュータシミュレーションあるいは数値解析は大変実用性の高い研究分野として注目を浴び,大きく成長してきました。現在,工学応用において数値流体力学を中核とするCAE(Computer Added Engineering)ツールは,どの業界にも欠かせない存在となっています。しかし,実応用から高い要望がある一方,多くの複雑な流れに対して物理現象を正しく再現できる計算手法や数値モデルはまだ確立されていません。引き続き様々な努力が必要です。
さらなる展開…
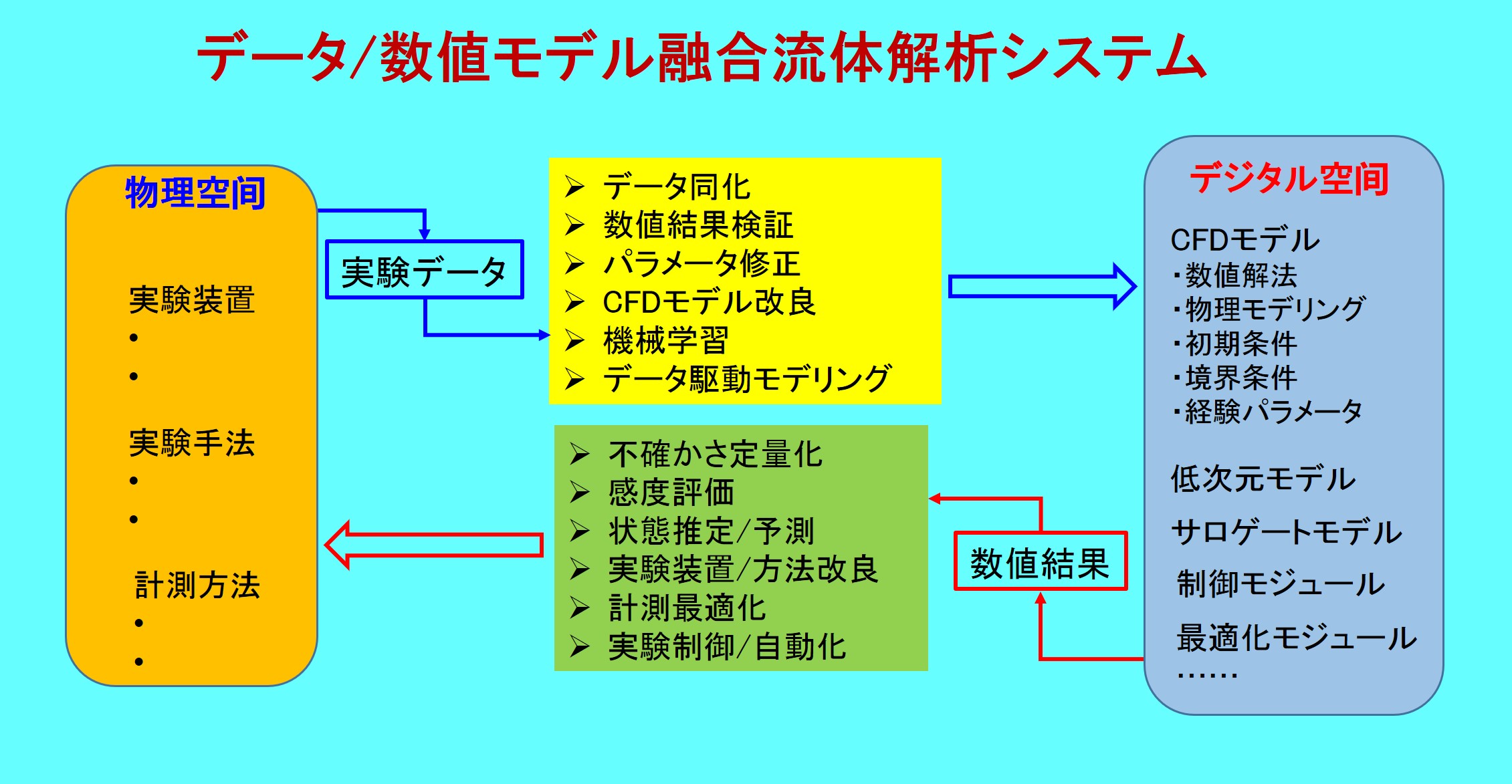
上述のシミュレーション手法は,決定論的なアプローチに基づくものですが,実現象を対象とする応用問題においては,様々な誤差や確定できない要素が存在します。これらの不確かさがシミュレーションの過程においてどのように伝播・変化するかは,数値計算結果の理解及び応用に非常に重要であり,適切に評価する必要があります。また,観測や実験計測で得られたデータを活用すれば,データ同化を通して数値モデルの不確かさを特定・修正することができます。逆に,数値解析モデルの結果から得られた各物理量の感度変化などの知見をもとに実験装置と計測方法の改良を図ることも可能になります。さらに,他分野と同様,利用可能な観測データ量が急速に拡大してきた現状を踏まえて,データと数値モデルを融合した流体解析は,実問題の解決に非常に有力なアプローチになりつつあります。
データと数値モデル融合した流体解析システムのイメージ
近年「TensorFlow」や「PyTorch」など機械学習のオープンソースライブラリが開発され,誰でも簡単に利用できるようになったため,ニューラルネットワークに代表される機械学習や人工知能の応用は様々な分野において急速に普及しています。学習データが十分であれば,物理法則/支配方程式を用いなくても(知らなくても)データの関連性を通して物事の因果関係を表せるデータ駆動型の計算モデルy=F(x)(広い意味での回帰モデル)の構築も可能となり,大きな注目を集めています。
「万能」ともいわれるニューラルネットワークは,非線形性が強く,複雑な流体現象の研究と応用にも非常に役に立つと考えられる一方,いかに高品質な学習データを取得し,さらにデータに含まれる情報を高効率で最大限に引き出しながら,既知の物理法則も活かせるような「最適な」学習コンフィグレーションを考案するかは大変重要な研究課題となります。
我々の研究について
様々複雑な流体現象を忠実に再現できる新しい計算手法、数値モデルを開発し、よりハイクオリティのy=F(x)を目指します。
Professor Xiao is among the World's Top 2% Scientists 2020 in Applied Mathematics研究の基本方針
関連分野の世界トップレベルの独創的な研究成果を目指す
実問題向けの数値解法・数値解析モデルの開発を重視する
特色的 / 社会関心度の高い / チャレンジングな研究を行う
個人能力を最大限に発揮できる研究テーマと研究環境を作る
主な研究方向
衝撃波や移動界面多相流などを含む複雑流体現象に対する高性能数値解法,数値解析モデルの開発
数値解析モデルにおける誤差及び不確かさの時間・空間における定量評価
データ同化,実験/数値モデルを融合した流体解析システムの構築と応用
機械学習・AI技術を援用した数値解析モデルの開発と応用
GPUなどアクセラレータを装備した並列コンピュータにおける高性能計算及び大規模シミュレーション
自然界及び工業応用における流動現象のモデリングと数値解析
など
シミュレーション結果ギャラリー
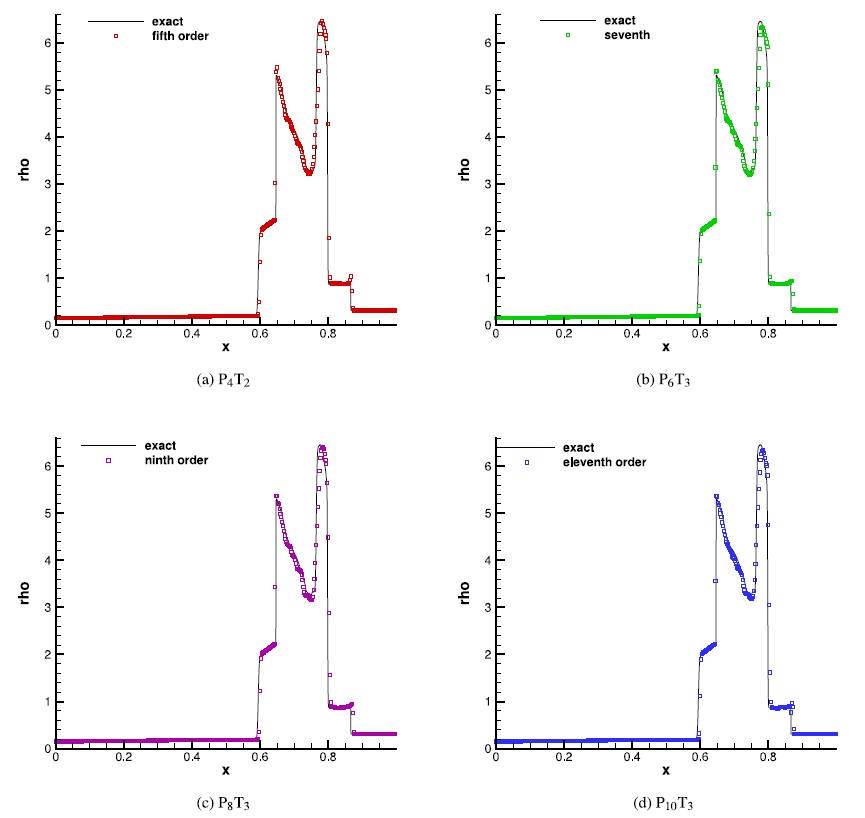
5次,7次,9次,11次精度BVD法による衝撃波干渉のベンチマークテスト結果(400メッシュ)。
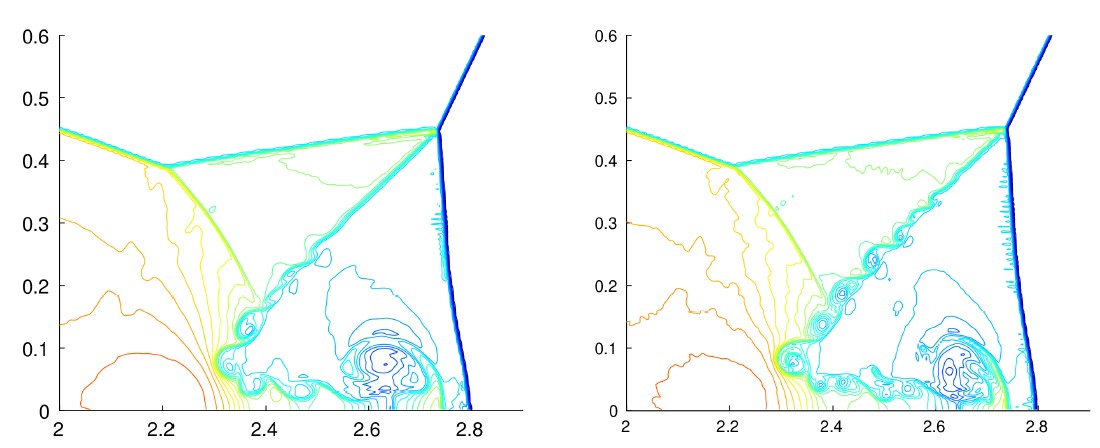
圧縮性流れのダブルマッハ反射ベンチマークテスト問題の計算結果(800×250メッシュ)。左:5次精度BVD法;右:15次精度BVD法。
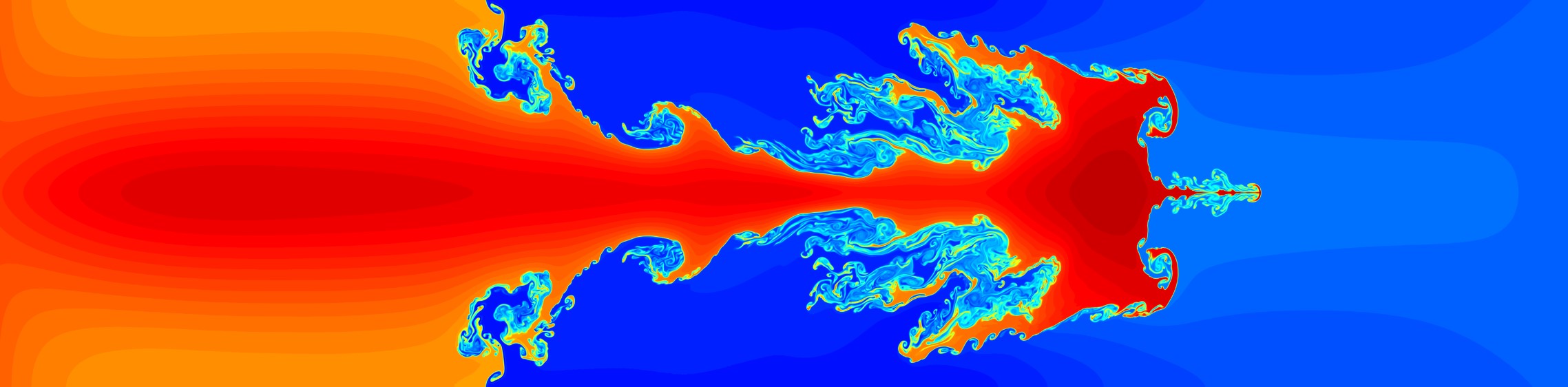
レイリー・テイラー不安定性テスト問題の計算結果(9600 x 4680メッシュ)。5次精度BVD法。
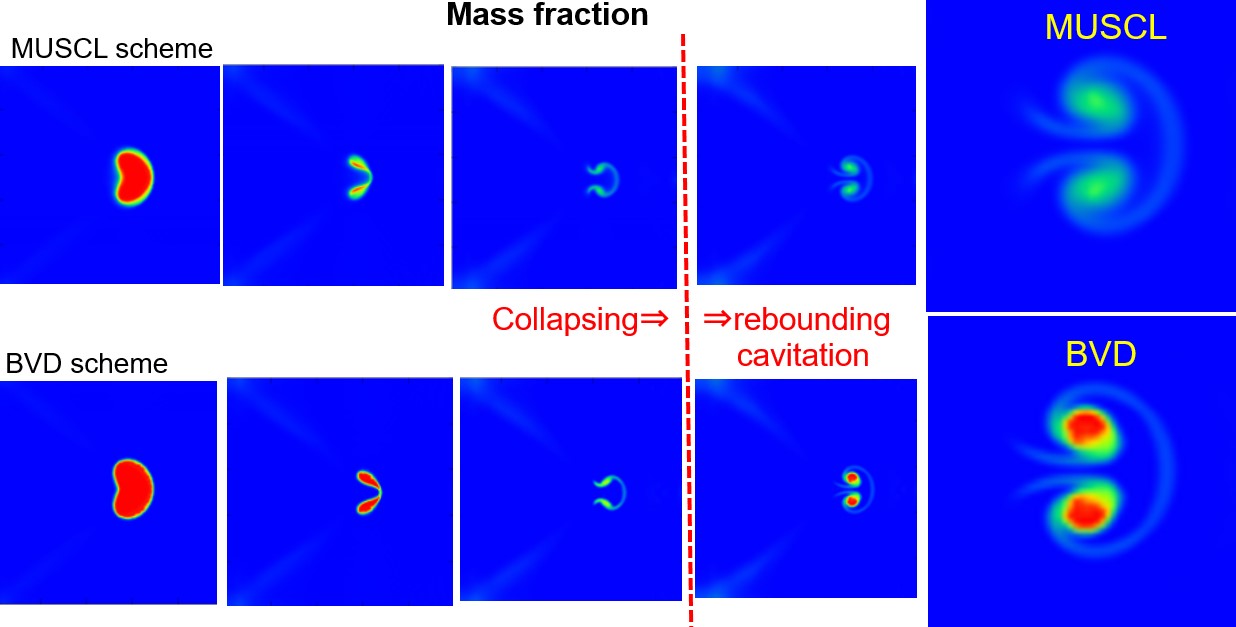
圧縮性気泡崩壊に伴うキャビテーション(蒸気化)現象。従来手法(MUSCL)が再現できない現象に対して,BVD法が鮮明に捉えている。
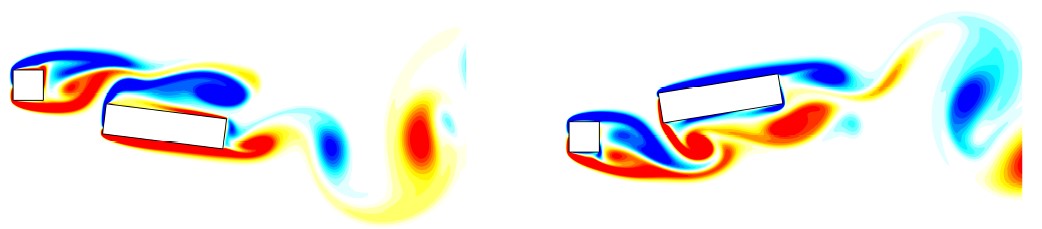
三角形障害物を通過する衝撃波。左:実験(Schardin,1965);右:VPM法。

VPM法による流体・構造体連成解析。
高温高速ガスジェット(MCV法)

水面に落下する物体[少しい昔の研究](CIP法を用いる統一解法+体積力による定式化) この結果は国際学術誌“Journal of Comutational Physics (vol.155,1999)”誌の表紙に使われた。20年以上前のことでしたが,当時はすごかった。

気液多相流界面における乱流輸送(VSIAM3に基づく統一解法+THNIC界面捕獲法)
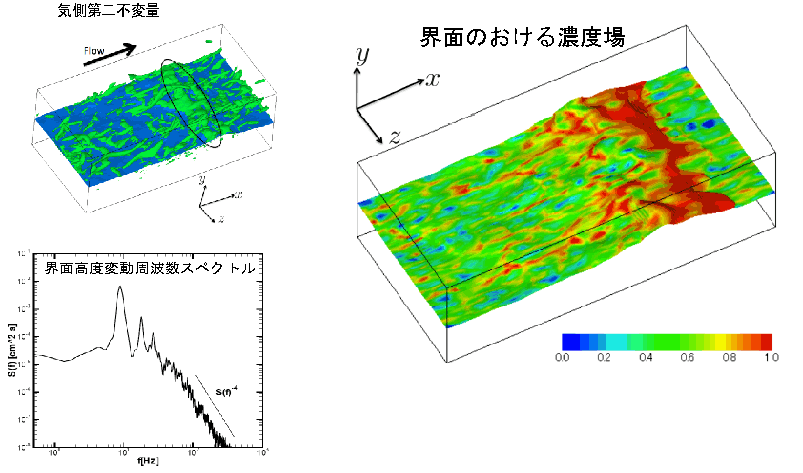
気泡・液滴など多相流現象のシミュレーション[少しい昔の研究](VSIAM3に基づく統一解法+界面捕獲法:STAA,THINC..)

マイクロチャンネル内の多相流(非構造VPM法+THNIC界面捕獲法)
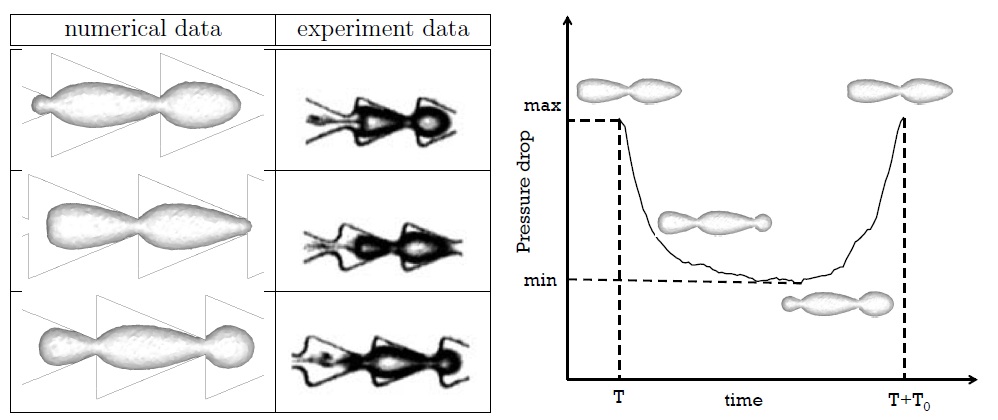
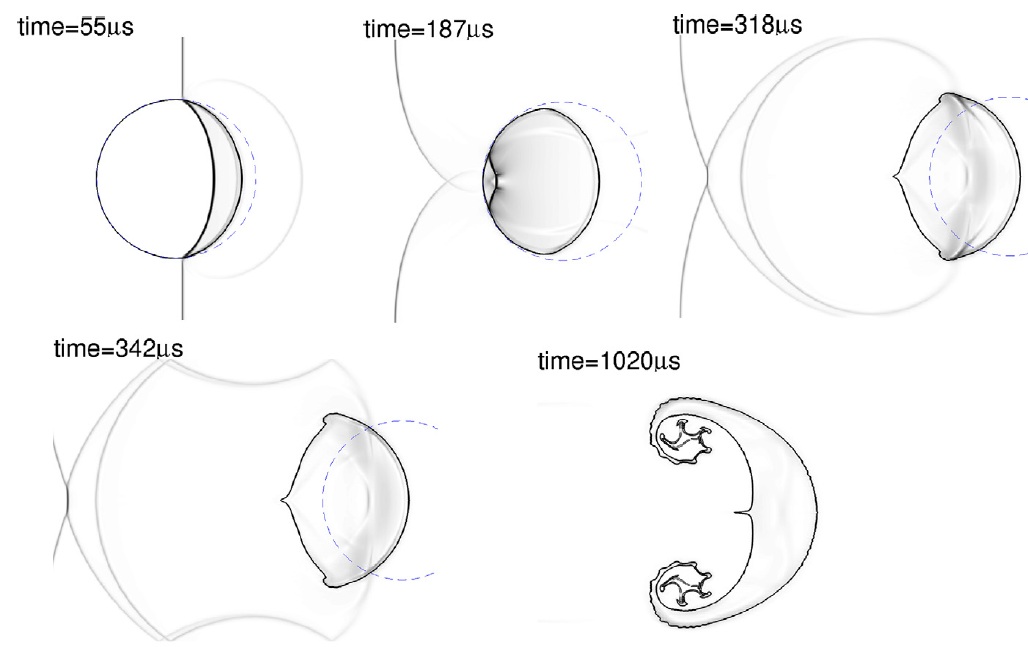
衝撃波と気泡の干渉・圧縮性自由界面多相流(FVM法+THNIC界面捕獲法)
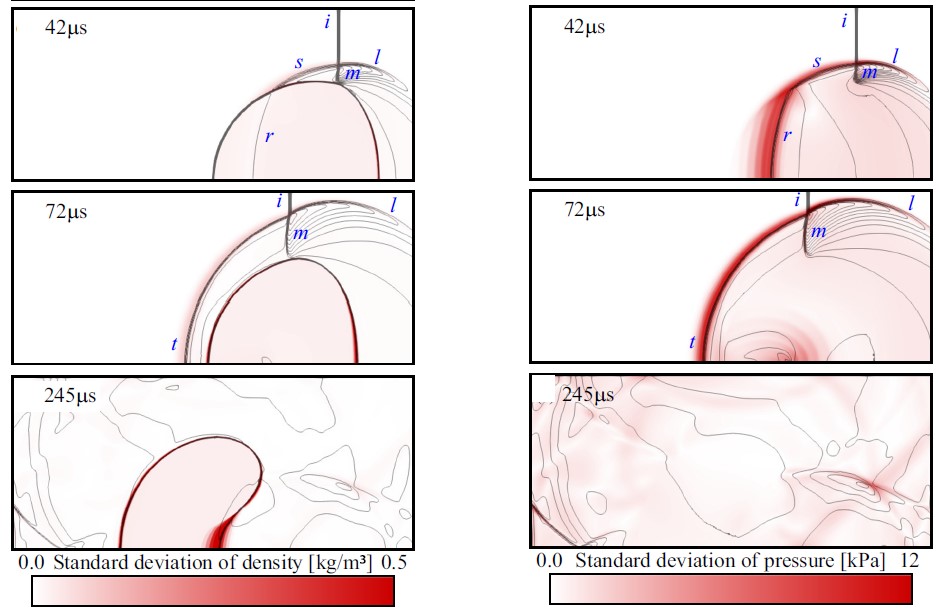
衝撃波/気泡干渉における気泡初期質量の不確かさのグローバル感度解析。
風力発電場風車レイアウトの最適化
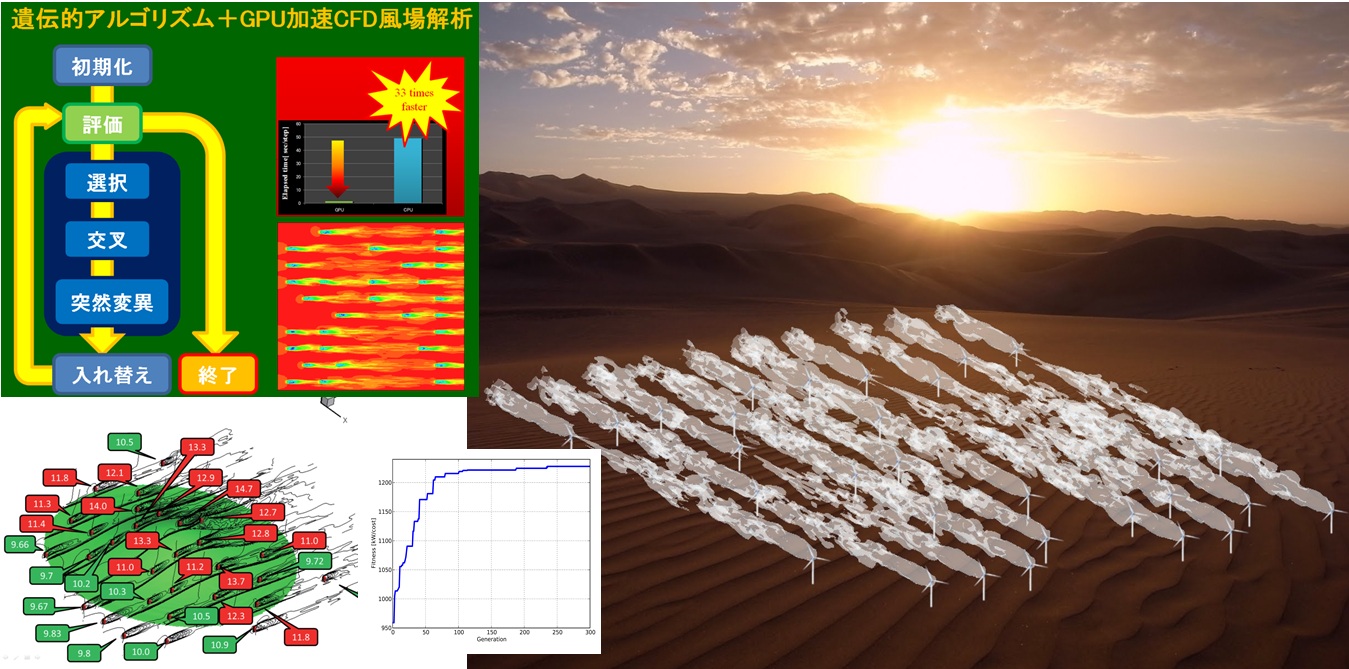
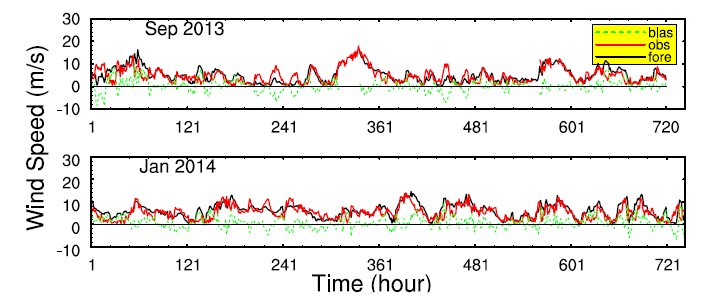
WRFモデルとカルマンフィルタによる風力発電予測
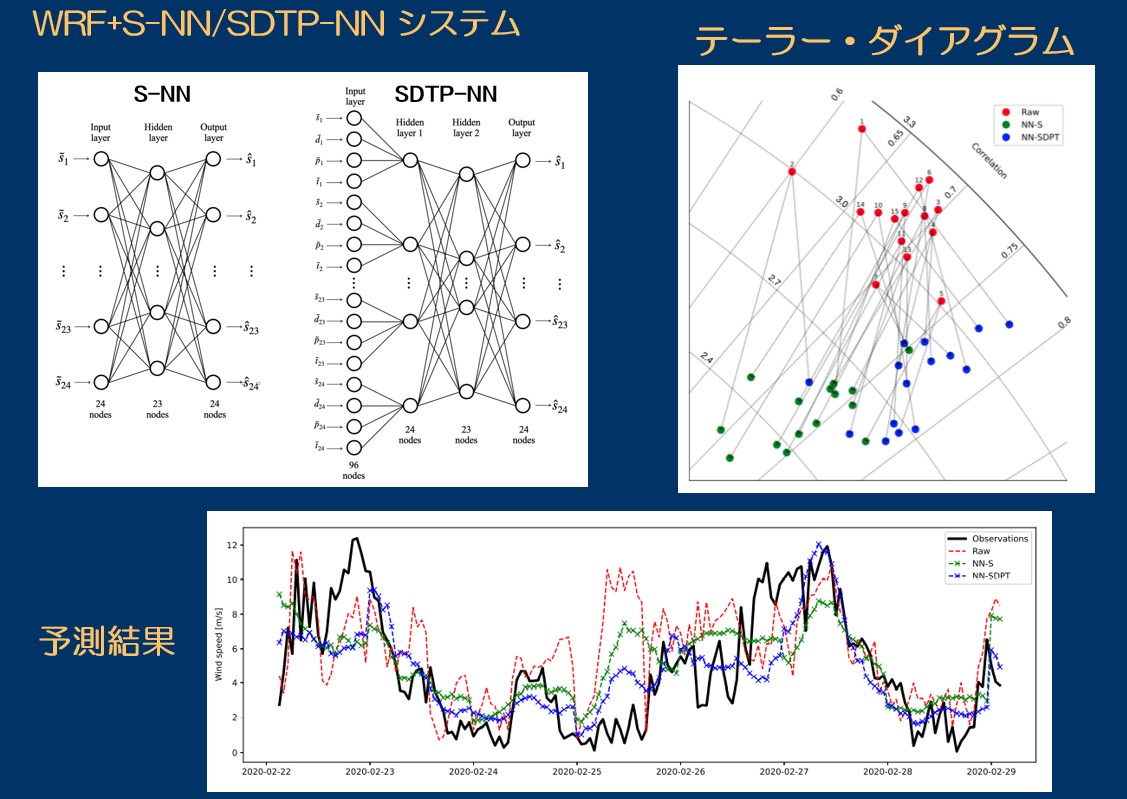
機械学習(ニューラルネットワーク)による風力発電予測システム
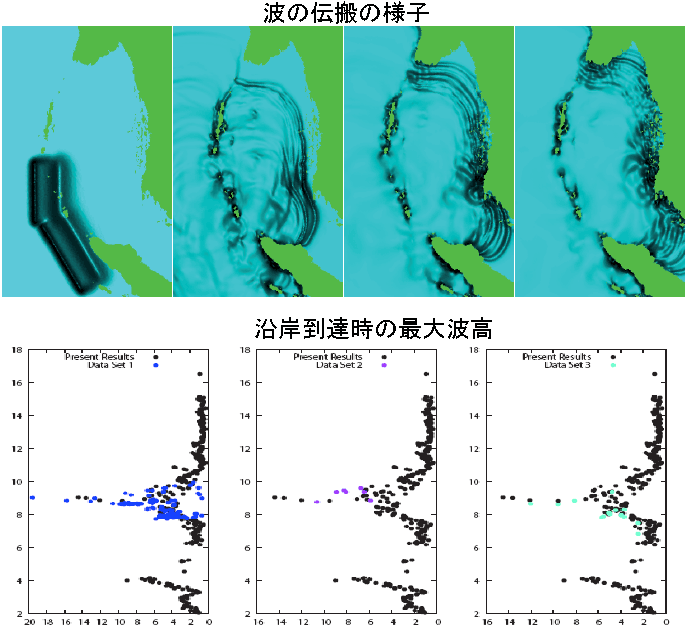
2004年インド洋大地震による津波シミュレーション(CIP/マルチモーメント有限体積法+非構造格子)
地球流体大循環モデル(マルチモーメント有限体積法)
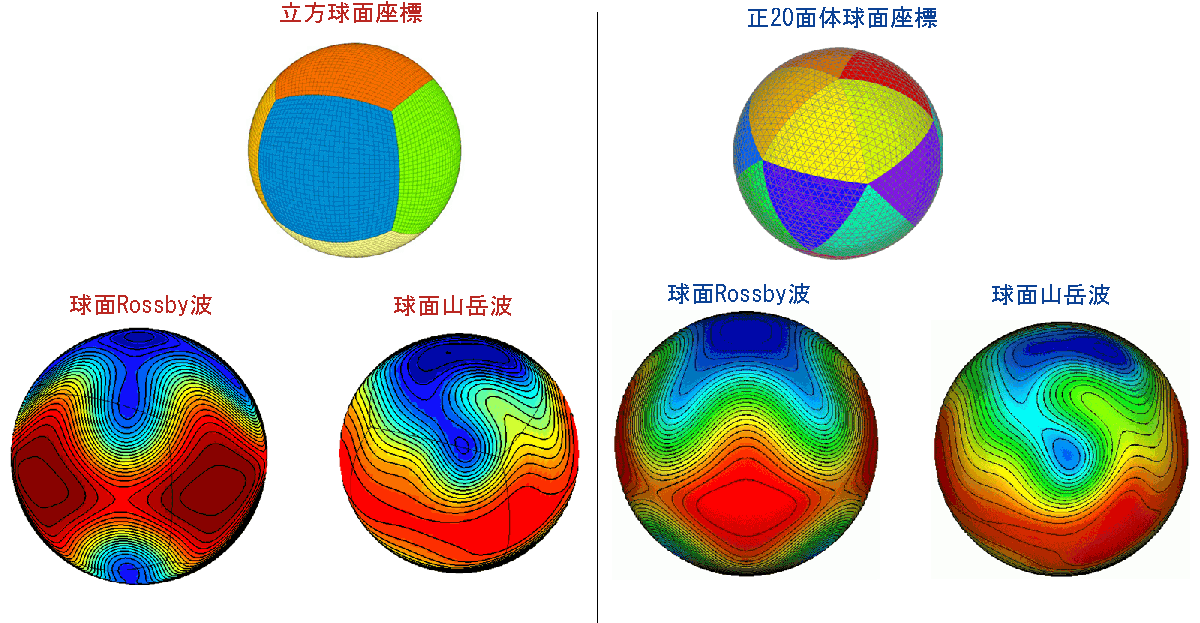
局域大気環境及び気象シミュレーション
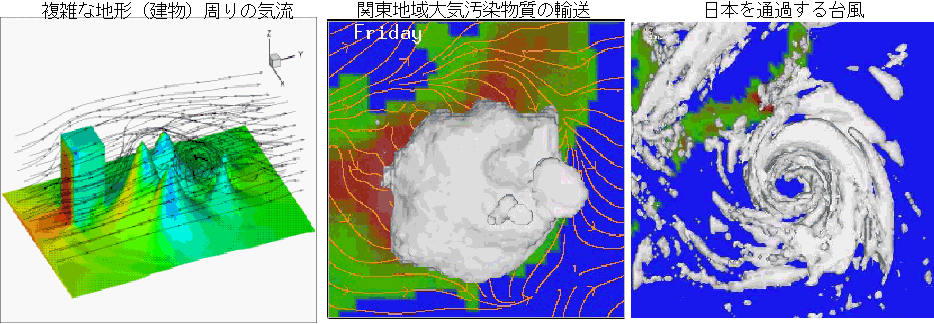
地球シミュレータスーパーコンピュータにおける大規模並列計算[少しい昔の研究]

